Метод от Мастера Ши Фэнчжи (石凤芝, Shífèngzhī).

人体 生命 数字 信息 手印.

"Отпечаток (Модель) цифровой информации о жизни человека".

Этот метод представляет собой простой, практичный, легкий в использовании и быстро действующий способ восстановления и поддержания здоровья, созданный на основе современной медицинской концепции функции самовосстановления человеческого тела. 

Благодаря различным формам, образованным вашими десятью пальцами, где сами руки используются в качестве полюсов электрического поля и магнитного поля человеческого тела, а также в качестве начальной и конечной точек шести меридианов трех ян руки и трех инь руки, регулирующих функцию человеческого тела. Фактически, большинство заболеваний являются результатом сбоя и нарушения функции саморегуляции. 

Слияние мудр (отпечатков пальцев) и цифровых кодов может не только корректировать положение и течение болезни, но и восстанавливать инстинкты здоровья организма.

Мастер Ши использует  цифры от "1" - 幺 (Yāo, "крышка") до "9", а также  и "0", но тут вместо "0" - 洞 (Dòng "дыра").

Мастер Ши использует вместо цифры "1" - 幺 (Yāo, Яо "Крышка"), а вместо "0" - 洞 (Dòng, Дун, "Дыра").

Дун вход в систему, Яо выход.

Практические инструкции от Мастера Ши Фэнчжи

1. Эти упражнение можно выполнять одновременно с другими упражнениями цигун.

2. Цифра «единица» "1" - 幺 (Yāo, "крышка") за цифровым кодом действует как ритм, и как музыкальный символ.

3. Выполняйте упражнения, чтобы вести себя совсем тихо, закройте глаза и сопоставьте числа с мудрой. Цифры беззвучно читаются в сердце («0» означает «дыра»- «洞 (дун)» , а "1" - "Крышка"«幺 (яо)»)

4. Эффект будет лучше, если вы сможете думать также о цвете числа одновременно с его прочтением.

5. Количество произнесенных цифр можно отсчитать по времени.

6. Собирая коды, произносите это «умом» и молчите 1– - 1 -- 1 — - - в своем сердце 3–4 раза.

7. Определите количество упражнений в соответствии с вашей физической подготовкой, но не более 5–6 раз.

8. Пациенты с несколькими заболеваниями могут сначала выбрать лечение одного своего основного заболевания, а затем они могут приступить к лечению от всего, но только после выздоровления.

9. Пациентам с психическими заболеваниями, неврозами и истерией не следует выполнять эти упражнения.

Более строгое определение Матрицы цифр, Информационной матрицы - 

информация по Фишеру,- матрица ковариаций информанта. Для доминированного семейства распределений вероятностей P^t(dw)с плотностями р(w; t), достаточно гладко зависящими от векторного (в частности, числового) параметра  элементы И. м. при t= q определяются как

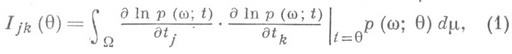
где j, k=1, . .., т. При скалярном параметре tИ. м. описывается единственным числом - дисперсией информанта.

И. м. I(q)определяет неотрицательную дифференциальную квадратичную форму

снабжающую семейство {Р ^t} римановой метрикой. Когда пространство Wисходов со конечно,

Дифференциальная квадратичная форма Фишера (2) является единственной (с точностью до постоянного множителя) дифференциальной квадратичной формой, инвариантной относительно категории статистических решающих правил. Ввиду этого она возникает в формулировке многих статистич. закономерностей.

Любое измеримое отображение f пространства Wисходов порождает новое гладкое семейство распределений Q^t=P^tf^-1 с И. м. I^Q(q). При этом И; м. монотонно не возрастает:

каковы бы ни были z_l, ..., z_m. И. м. обладает также свойством аддитивности. Если I⁽ⁱ⁾(q) (9) - И. м. для семейства с плотностью Р _i((wⁱ; t), то для семейства

будет  В частности, I_N(q)=NI(q). при Nнезависимых одинаково распределенных испытаниях. И. м. позволяет охарактеризовать статистич. точность решающих правил в задаче оценки параметра закона распределения. Для дисперсии любой несмещенной оценки t(w)=т(w⁽¹⁾, ..., w^(N)) скалярного параметра tсправедливо

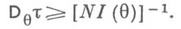
Аналогичное матричное неравенство информации выполняется для оценок векторного параметра. Его скалярное следствие

показывает, что несмещенное оценивание нигде не может быть слишком точным. Для произвольных оценок последнее неверно. Однако остаются ограничения, напр., на среднюю точность

где усреднение левой части (3) проведено по инвариантному объему Vлюбой компактной подобласти

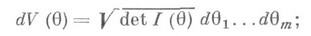
остаточный член зависит от размеров Q'. Неравенства (4) асимптотически точны, и асимптотически оптимальной в этом смысле оказывается оценка максимума правдоподобия.

В точках вырождения, det I(q)=0, совместная оценка параметров затруднена; если det I(q) = 0 в нек-рой области, то совместная оценка вообще невозможна. Таким образом, следуя Р. Фишеру [1], с известной осторожностью можно сказать, что И. м. описывает среднее количество информации о параметрах закона раейределения, содержащееся в случайной выборке.